Last version published: 24/01/2017 15:49
Publication number: ELQ-76537-4
View all versions & Certificate

Option Value with Black-Scholes formula
Find the value of puts, calls, and combinations of options using the Black-Scholes formula.
Prof. Richard L. Smith offers you this Best Practice for free!
download for free
Add to bookmarks
Further information
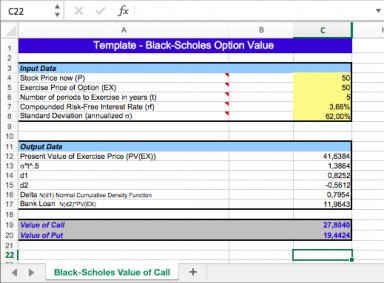
Required input data:
- Stock Price now
- Exercise Price of Option
- Number of periods to Exercise in years
- Compounded Risk-Free Interest Rate
- Standard Deviation
Produced output:
- Present Value of Exercise Price
- s*t^.5
- d1
- d2
- Delta N(d1) Normal Cumulative Density Function
- Bank Loan N(d2)*PV(EX)
Results:
- Value of Call
- Value of Put
The Option Pricing Model depends on market completeness, continuous trading, normally distributed risk, independence, and other factors to derive option values. When these assumptions are violated (as they usually are for new ventures and for real options), formal valuation approaches can still provide insights, but the actual values of options are less certain. It is common to employ simulation and numerical methods to value options when critical assumptions are not satisfied"
(An Introduction to Options, Entrepreneurial Finance, by Janet Kilholm SMith, Richard L. Smith and Richard T. Bliss)